11. Uncertainty Estimation
Uncertainty Estimation
ND320 AIHCND C01 L04 A09 Uncertainty Estimation
Uncertainty Estimation Key Points
Why use Uncertainty Estimation?
A typical classification problem provides predictions with relative weightings across the prediction classes and is different than the confidence in a given prediction. Uncertainty estimation helps us with this.
Class Probabilities != confidence in a prediction.
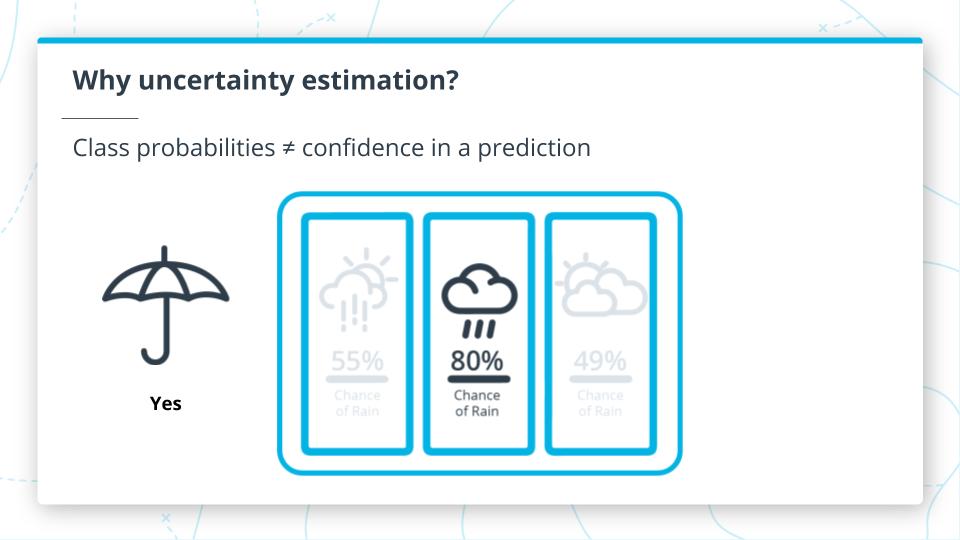
Uncertainty Weather Example
Example:
Which is better?
- A weather forecast with a simple Yes or No prediction it will rain with some icons?
- A forecast that also provides the percent chance of rain or how certain the model is of its prediction?
Most people would prefer the second one and in healthcare this even more important.
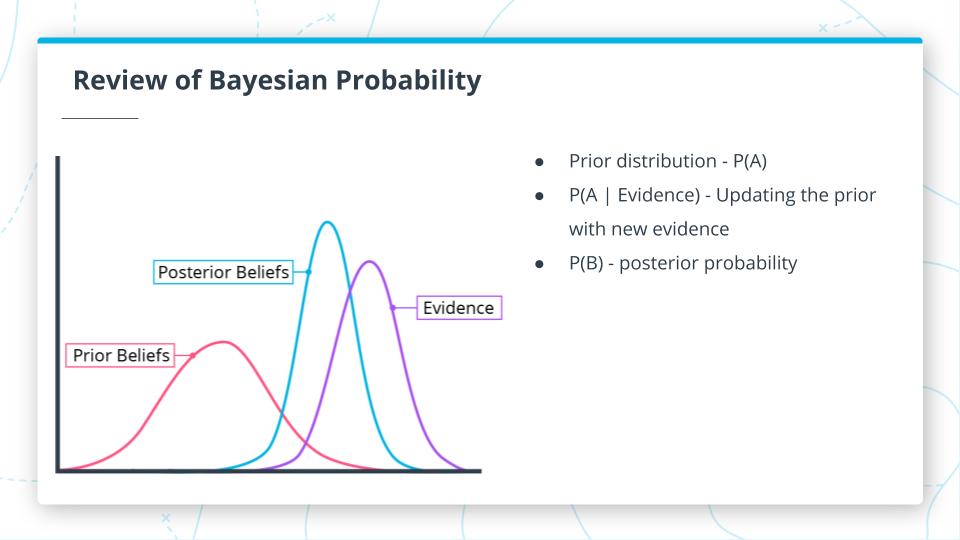
Review of Bayesian Probability
Bayesian Probability Review
Probabilistic Programming
To address uncertainty estimation we can use probabilistic programming, in particular, we can create Bayesian Neural Networks (BNN) using TensorFlow Probability. TF probability combines Bayesian probabilistic approaches with deep learning and since it is built on Tensorflow you can train with GPUs too.
Bayesian statistical approaches can be very helpful for situations where you can leverage deep domain knowledge and have small datasets. Healthcare is an industry where you might have small datasets on patient data for a new drug or rare conditions. Also, healthcare is a field where you can leverage deep domain knowledge from medical professionals and medical literature which can help provide positive “bias” in your model with pertinent domain knowledge.
Review of Bayesian Probability
- Prior distribution - P(A)
- P(A | Evidence) - Updating the prior with new evidence
- P(B) - posterior probability
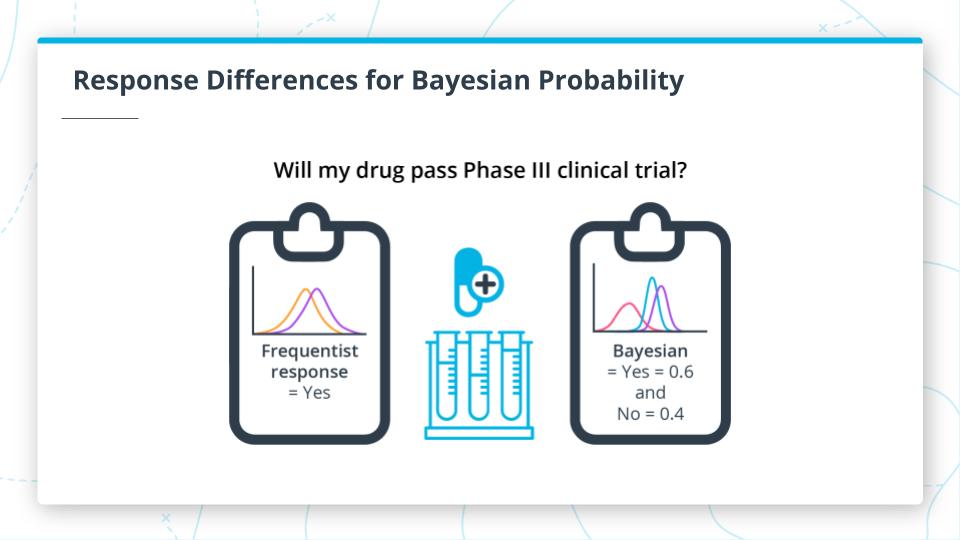
Response Differences for Bayesian Probability
Example:
Let’s say we want to assess whether a drug will pass a phase III clinical trial. The frequentist statistical response would be a yes or no response. However, the bayesian response would give a yes/no and the certainty/confidence in that prediction. This can be helpful when connecting it with metrics like Brier scores that can combine predictions from various models.
If you are only 51% certain that you will pass the clinical trial, how certain would you be?
SOLUTION:
- Tensorflow Probability combines Bayesian probabilistic approaches with deep learning.
- Bayesian approaches can be useful when you have small datasets with deep domain knowledge.